Question

In the months leading up to an election, news organizations conduct many surveys to help predict the results of the election. Often news organizations will increase the sample size in the last few weeks before the election. Which of the following is the primary reason they increase the sample size?

A larger sample size allows more people to give their input.
A larger sample size means the sampling method isn’t as important.
A larger sample size gives a higher confidence level.
A larger sample size gives a narrower confidence interval.

Answer 1

For this problem we need to take in count that in elections the parameter of interest is a proportion and the margin of error for this parameter is given by:

`ME = z_(\alpha/2) \sqrt{(\hat p(1-\hat p))/(n)}`

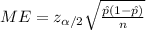
And we need to take in count that if the margin of error increase the lenght of the confidence interval increase and otherwise decrease.

For this problem if we increase the sample size n then the denominator for the margin of error would decrease and the resultant effect would be:

A larger sample size gives a narrower confidence interval.

Explanation:

For this problem we need to take in count that in elections the parameter of interest is a proportion and the margin of error for this parameter is given by:

`ME = z_(\alpha/2) \sqrt{(\hat p(1-\hat p))/(n)}`

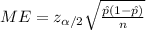
And we need to take in count that if the margin of error increase the lenght of the confidence interval increase and otherwise decrease.

For this problem if we increase the sample size n then the denominator for the margin of error would decrease and the resultant effect would be:

A larger sample size gives a narrower confidence interval.