Question

With data from the 2009 National Health Interview Survey, the Centers for Disease Control estimated that 9.4% of U.S. children had asthma. Suppose that 12% of a random sample of 500 U.S. poor children have asthma. We used the estimate from the 2009 National Health Interview Survey to calculate a standard error of 0.013. The data allows the use of a normal model. So we can find an approximate 95% confidence interval for the percentage of all U.S. poor children who have asthma. Which interval is the approximate 95% confidence interval? Group of answer choices

0.094 to 0.146
0.107 to 0.133
0.026 to 0.214
0.068 to 0.12

Answer 1

`0.12 -1.96*0.013= 0.094`

`0.12 +1.96*0.013= 0.146`

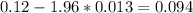
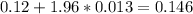
And the best option would be:

0.094 to 0.146

Explanation:

For this case we have the following info given:

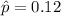`\hat p=0.12` represent the proportion estimated

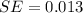`SE = 0.013` represent the standard error

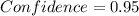`Confidence =0.95` represent the confidence level

The confidence interval for the true proportion is given by:

`\hat p \pm z_(\alpha/2) SE`

And for 95% of confidence the critical value is
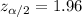`z_(\alpha/2)= 1.96` and replacing we got:

`0.12 -1.96*0.013= 0.094`

`0.12 +1.96*0.013= 0.146`

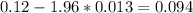
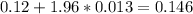
And the best option would be:

0.094 to 0.146