Question

Find maximum points y=11^(6x-x²) solve using derivative

Answer 1

`\boxed{\sf \ \ \ maximum \ is \ 11^9=2357947691 \ \ \ }`

Explanation:

hello

`y = 11^((6x-x^2))=exp((6x-x^2)ln(11))`

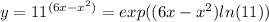
so to know the maximum to y we can check the maximum of

f(x)=
`6x-x^2`

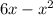
f is derivable and f'(x)=6-2x

f'(x)=0 <=> x = 3

so the maximum is reached for x = 3

f(3)=18-9=9

and then

`y = 11^9=2357947691`

to be rigorous, we can write the variation table of y to show that there is only one maximum

hope this helps