Answer:
a)0.654
b)-0.34
Explanation:
a)2 3 4 5 6 7
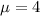
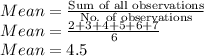
Standard deviation
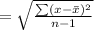
Standard deviation
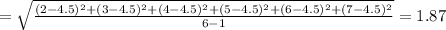
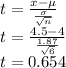
Df = n-1 = 6-1 = 5
Assume α=0.05
So
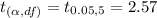
So, t critical = 2.57
So, t calculated < t critical
b)1 2 2 5 5 7
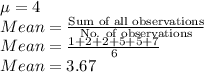
Standard deviation =
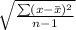
Standard deviation =
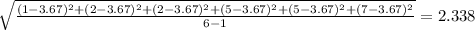
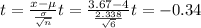
Df = n-1 = 6-1 = 5
Assume α=0.05
So,
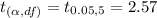
So, t critical = 2.57
So, t calculated < t critical