Question

Find parametric equations for the line through point P(-1,-1,-1) and Q(-5,7,3) A. x = t + 4; y = t - 8; z = -1t - 4

B. x = -4t - 1; y = 8t - 1; z = 4t - 1
C. x = -4t + 1; y = 8t + 1; z = 4t + 1
D. x = t - 4; y = t + 8; z = -t + 4

Answer 1

B) x = -4t - 1; y = 8t - 1; z = 4t - 1

Explanation:

Explanation:-

Given points are P(-1,-1,-1) and Q(-5,7,3)

Let (x₁ , y₁ , z₁) = P(-1,-1,-1)

Let (x₂ , y₂ , z₂) = Q(-5,7,3)

Parametric equation of the line passing through the points (x₁ , y₁ , z₁) and (x₂ , y₂ , z₂)

`(x-x_(1) )/(x_(2)-x_(1) ) = (y-y_(1) )/(y_(2)-y_(1) ) = (z-z_(1) )/(z_(2)-z_(1) ) = t`

`(x-(-1))/(-5-(-1)) = (y -(-1))/(7-(-1)) = (z-(-1))/(3-(-1)) = t`

`(x-(-1))/(-4) = (y -(-1))/(8) = (z-(-1))/(4) = t`

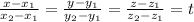
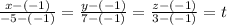
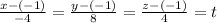
Equating each term

`(x+1)/(-4) = t`

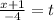
⇒ x + 1 = - 4 t

⇒ x = - 4 t -1

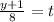
`(y +1)/(8) = t`

y + 1 = 8 t

⇒ y = 8 t - 1

`(Z+1)/(4) =1`

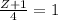
⇒ z +1 = 4t

⇒ z = 4t -1

Final answer:-

parametric equations for the line through point P(-1,-1,-1) and Q(-5,7,3)

are

x = -4t - 1; y = 8t - 1; z = 4t - 1