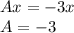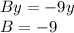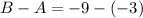Question

Find the value of B - A if the graph of Ax + By = 3 passes through the point (-7, 2), and is parallel to the graph x + 3y = -5. Pls help ASAP btw, the answer isn’t -12/19 or 12/19

Answer 1

`B - A = -6`

Explanation:

Given

Point: (-7,2)

x + 3y = -5

Required

Find B- - A in Ax + By = 3

To start with; we need to calculate the slope of x + 3y = -5

`x + 3y = -5`

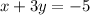
Subtract x from both sides

`x - x + 3y = -5 - x`

`3y = -5 - x`

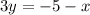
Divide both sides by 3

`(3y)/(3) = -(5)/(3) - (x)/(3)`

`y = -(5)/(3) - (x)/(3)`

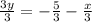
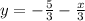
The slope of the line is the coefficient of x

Slope =
`- (1)/(3)`

The question says line Ax + By = 3 is parallel to line x + 3y = -5; This means that they have the same slope of
`- (1)/(3)`

Having calculated the slope, next is to calculate the equation of the line using the following formula;

`m = (y - y_1)/(x - x_1)`

Where m is the slope; m =
`- (1)/(3)`;
`(x_1, y_1) = (-7,2)`

Substitute these values in the formula above; the formula becomes

`-(1)/(3) = (y - 2)/(x - -7)`

`-(1)/(3) = (y - 2)/(x +7)`

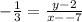
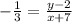
Cross Multiply

`-1(x+7) = 3(y-2)`

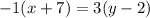
Open brackets

`-x - 7 = 3y - 6`

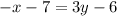
Add x to both sides

`x - x - 7 = 3y - 6 + x`

`-7 = 3y - 6 +x`

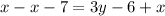
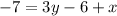
Add 6 to both sides

`-7 + 6 = 3y -6 + 6 + x`

`-1 = 3y + x`

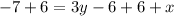
Multipby both sides by -3

`-3(-1) = -3(3y + x)`

`3 = -9y - 3x`

`-9y - 3x = 3`

`-3x - 9y = 3`

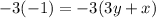
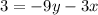
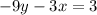
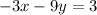
Comparing the above to Ax + By = 3

`Ax = -3x\\A = -3`

`By = -9y\\B = -9`

`B - A = -9 - (-3)`

`B - A = -9 + 3`

`B - A = -6`