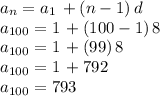Answer:
The 100th term is 793.
Explanation:
Notice that this arithmetic sequence has first term
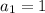
and common difference
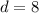 (since each consecutive term is built by adding "8" to the previous one)
(since each consecutive term is built by adding "8" to the previous one)
Recall the general formula for the nth term of a sequence:
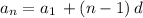
therefore, for our articular case, the term 100th can be obtained with: