Answer:
The probability of drawing the compliment of a king or a queen from a standard deck of playing cards = 0.846
Explanation:
Step(i):-
Let 'S' be the sample space associated with the drawing of a card
n (S) = 52C₁ = 52
Let E₁ be the event of the card drawn being a king
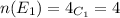
Let E₂ be the event of the card drawn being a queen

But E₁ and E₂ are mutually exclusive events
since E₁ U E₂ is the event of drawing a king or a queen
step(ii):-
The probability of drawing of a king or a queen from a standard deck of playing cards
P( E₁ U E₂ ) = P(E₁) +P(E₂)
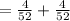
P( E₁ U E₂ ) =
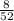
step(iii):-
The probability of drawing the compliment of a king or a queen from a standard deck of playing cards
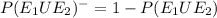

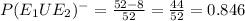
Conclusion:-
The probability of drawing the compliment of a king or a queen from a standard deck of playing cards = 0.846