Answer:
a) The length of the building that should border the dog run to give the maximum area = 25feet
b) The maximum area of the dog run = 1250 s q feet²
Explanation:
Step(i):-
Given function
A(x) = x (100-2x)
A (x) = 100x - 2x²...(i)
Differentiating equation (i) with respective to 'x'
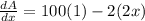
⇒
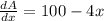 ...(ii)
...(ii)
Equating zero
⇒ 100 - 4x =0
⇒ 100 = 4x
Dividing '4' on both sides , we get
x = 25
Step(ii):-
Again differentiating equation (ii) with respective to 'x' , we get
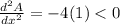
Therefore The maximum value at x = 25
The length of the building that should border the dog run to give the maximum area = 25
Step(iii)
Given A (x) = x ( 100 -2 x)
substitute 'x' = 25 feet
A(x) = 25 ( 100 - 2(25))
= 25(50)
= 1250
Conclusion:-
The maximum area of the dog run = 12 50 s q feet²