Answer:
a)
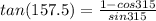
b)
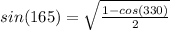
c)
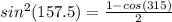
d)
cos 330° = 1- 2 sin² (165°)
Explanation:
Step(i):-
By using trigonometry formulas
a)
cos2∝ = 2 cos² ∝-1
cos∝ = 2 cos² ∝/2 -1
1+ cos∝ = 2 cos² ∝/2
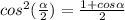
b)
cos2∝ = 1- 2 sin² ∝
cos∝ = 1- 2 sin² ∝/2
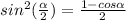
Step(i):-
Given
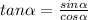
we know that trigonometry formulas
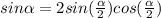
1- cos∝ = 2 sin² ∝/2
Given
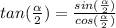
put ∝ = 315
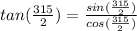
multiply with ' 2 sin (∝/2) both numerator and denominator
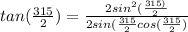
Apply formulas
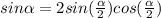
1- cos∝ = 2 sin² ∝/2
now we get
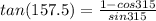
b)
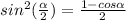
put ∝ = 330° above formula
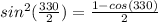
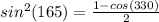
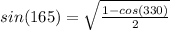
c )
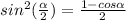
put ∝ = 315° above formula
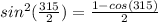
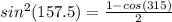
d)
cos∝ = 1- 2 sin² ∝/2
put ∝ = 330°
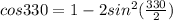
cos 330° = 1- 2 sin² (165°)