Question

A questionnaire about study habits was given to a random sample of students taking a large introductory stats class. The sample of 35 students reported that they spent an average of 115 minutes per week studying stats. Assume that the standard deviation is 40 minutes.A) Give a 95% confidence interval for the mean time spent studying stats by students in this class.B) Is it true that 95% of the students in the class have weekly studying times that lie in the interval you found in (A)? Explain

Answer 1

(a) The 95% confidence interval for the mean time spent studying stats is (101.75, 128.25).

(b) TRUE.

Explanation:

Let the random variable X represent the time spent per week studying stats.

The information provided is:

`\bar x=115\\\sigma=40\\n=35\\\alpha=0.05`

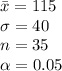
(a)

The (1 - α)% confidence interval for the population mean is:

`CI=\bar x\pm z_(\alpha/2)\cdot (\sigma)/(√(n))`

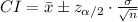
The critical value of z for 95% confidence level is, z = 1.96.

Compute the 95% confidence interval for the mean time spent studying stats as follows:

`CI=\bar x\pm z_(\alpha/2)\cdot (\sigma)/(√(n))`

`=115\pm 1.96\cdot (40)/(√(35))\\\\=115\pm13.252\\\\=(101.748, 128.252)\\\\\approx (101.75, 128.25)`

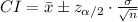
Thus, the 95% confidence interval for the mean time spent studying stats is (101.75, 128.25).

(b)

The true mean time spent studying stats by students in this class is contained in the 95% confidence interval, (101.75, 128.25) with a probability of 0.95.

The sample mean time spent studying stats is,
`\bar x=115\ \text{minutes}`.

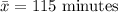The law of large numbers, in probability concept, states that as we increase the sample size, the mean of the sample (
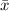`\bar x`) approaches the whole population mean (µ).

The sample size selected here is (n = 35 > 30) quite large.

So according to the law of large numbers the population mean is approximately 115 minutes.

And since the population mean is contained in the interval, it can be said that 95% of the students in the class have weekly studying times that lie in the interval (101.75, 128.25).