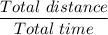Question

Two boats leave port at noon. Boat 1 sails due east at 12 knots. Boat 2 sails due south at 8 knots. At 2 pm the wind diminishes and Boat 1 now sails at 9 knots. At 3 pm, the wind increases for Boat 2 and it now sails 7 knots faster. How fast (in knots) is the distance between the two ships changing at 5 pm. (Note: 1 knot is a speed of 1 nautical mile per hour.)

Answer 1

14.86 knots.

Explanation:

Given that:

The boats leave the port at noon.

Speed of boat 1 = 12 knots due east

Speed of boat 2 = 8 knots due south

At 2 pm:

Distance traveled by boat 1 = 24 units due east

Distance traveled by boat 2 = 16 units due south

Now, speed of boat 1 changes to 9 knots:

At 3 pm:

Distance traveled by boat 1 = 24 + 9= 33 units due east

Distance traveled by boat 2 = 16+8 = 24 units due south

Now, speed of boat 1 changes to 8+7 = 15 knots

At 5 pm:

Distance traveled by boat 1 = 33 + 2
`*` 9= 51 units due east

Distance traveled by boat 2 = 24 + 2
`*` 15 = 54 units due south

Now, the situation of distance traveled can be seen by the attached right angled
`\triangle AOB`.

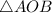O is the port and A is the location of boat 1

B is the location of boat 2.

Using pythagorean theorem:

`\text{Hypotenuse}^(2) = \text{Base}^(2) + \text{Perpendicular}^(2)\\\Rightarrow AB^(2) = OA^(2) + OB^(2)\\\Rightarrow AB^(2) = 51^(2) + 54^(2)\\\Rightarrow AB^(2) = 2601+ 2916 = 5517\\\Rightarrow AB = 74.28\ units`

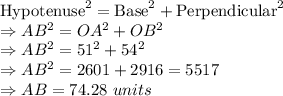
so, the total distance between the two boats is 74.28 units.

Change in distance per hour =
`(Total\ distance)/(Total\ time)`

`\Rightarrow (74.28)/(5) = 14.86\ knots`