Question

Having aced your introductory physics course, you are hired as a summer intern at NASA. You are sent as part of a team to explore the possibility of mining iron from a small, airless spherical asteroid with a radius of 499 km and a surface acceleration of 2.6 m/sec2.

1) What is the mass of the asteroid?
2) What is the minimum vertical velocity you could give a 4 kg rock from the surface of this asteroid so that it continues to move upwards forever (i.e. it would never return to the surface)?
3) What is the minimum vertical velocity you could give an 8 kg rock from the surface of this asteroid so that it continues to move upwards forever (i.e. it would never return to the surface)?
4) How far will the 4 kg rock go if it leaves the asteroid's surface with a vertical velocity of 1000 m/s?
5) What will the speed of the 8 kg rock be at the surface of the asteroid if it is dropped from a point 1000 km above the surface of the asteroid?

Answer 1

1) M = 9.7*10^21 kg

2, 3) 1610.81 m/s

4) 312.911 km

5) 1315.65 m/s

Step-by-step explanation:

Given:-

- The radius of the asteroid, R = 499 km

- The surface acceleration, g = 2.6 m/s^2

Solution:-

- To determine the mass of the asteroid ( M ) we will use the relation for the gravitational acceleration produced by a spherical object of mass ( M ) as follows:

`g = G(M)/(R^2)`

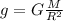
Where,

G: the universal gravitational constant = 6.674*10^−11

- Use the radius of asteroid ( R ) and the given surface acceleration ( g ) and solve for the mass ( M ) of the asteroid using the relation given above:

`M = (gR^2)/(G) \\\\M = (2.6*(499,000)^2)/(6.674*10^-^1^1) \\\\M = 9.7*10^2^1 kg`

- To determine the escape velocity of the mass of rock ( m = 4kg ) from the gravitational pull of the asteroid. We will use the conservation of energy principle.

- The conservation of energy principle states:

`K.E_i + P.E_i = K.E_f + P.E_f`

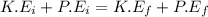
Where,

K.Ei: The initial kinetic energy of the rock of mass ( m )

P.Ei: The potential energy of the system at the surface

K.Ef: The final kinetic energy of the rock of mass ( m )

P.Ef: The final potential energy of the system at infinite

- The gravitational potential energy of the system of an object of mass (m ) at any distance ( r ) from the center of the more massive body ( M ) is given as:

`P.E = - G(M*m)/(r)`

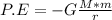
- The escape velocity is just enough initial velocity ( ve ) that allows an object to cross the gravitational effect of the massive body. Once the effect of the gravity is insignificantly small ( infinite ). Almost all of the kinetic energy has been lost by doing work against the gravitational pull.

- Therefore, K.Ef = P.Ef = 0 ( at infinity ).

`0.5mv_e^2 - G(Mm)/(r) = 0\\\\v_e = \sqrt{2G(M)/(r) } = \sqrt{2G(M)/(R) } \\\\v_e = \sqrt{2(6.674*10^-^1^1)(9.7*10^2^1)/(499,000) }\\\\v_e = 1610.81 (m)/(s)`

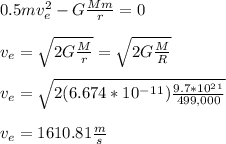
- From the above relationship derived for an object at the surface of an asteroid body to escape the grasp of the gravitational pull is independent of the mass of the object ( m ). Hence, whatever the mass of the object is it does not affect the required escape velocity.

Answer: The rock of mass m = 8 kg and m = 4 kg require minimum vertical velocity of 1610.81 m/s to escape the asteroid gravitational pull.

- For the final part we will again apply the principle of conservation of energy for the system of asteroid of mass ( M ) and an object of mass ( m ). We have:

`K.E_i + P.E_i = K.E_f + P.E_f`

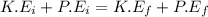
Where,

K.Ei: The initial kinetic energy of the rock of mass ( m ) = 0 ( dropped)

P.Ei: The potential energy of the system at altitude ( h )

K.Ef: The final kinetic energy of the rock of mass ( m ) at surface

P.Ef: The final potential energy of the system at surface

`0 - G(Mm)/(( R + h )) = 0.5mv^2 - G(Mm)/( R ) \\\\v^2 = 2GM* [ (1)/(R) - (1)/(R+h) ] \\\\v = \sqrt{2(6.674*10^-^1^1)*(9.70*10^2^1)* [ (1)/(499,000) - (1)/(1499000)]}\\\\v = 1315.65 (m)/(s)`

Answer: The speed of the 8kg rock upon hitting the surface of asteroid would be 1315.65 m/s

- Similarly, how far away a rock of mass ( m ) can go to from the surface of asteroid if it leaves the surface with initial velocity vi = 1000 m/s. We will use the energy conservation expression derived in the previous part. We have:

`0.5mv^2 - G(Mm)/(R) = G(Mm)/(R + h) \\\\(0.5v^2)/(GM) - (1)/(R) = -(1)/(R + h)\\\\R + h = (1)/(-(0.5v^2)/(GM) + (1)/(R)) \\\\h = (1)/(-(0.5v^2)/(GM) + (1)/(R)) - R\\\\h = (1)/(-(0.5(1000)^2)/((6.674*10^-^1^1)*(9.7*10^2^1)) + (1)/((499000))) - 499000\\\\h = 312.911 km`

Answer: The 4 kg rock would be able to travel 312.911 km above the asteroid surface if it had an initial velocity of 1000 m/s.