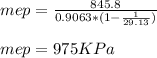Question

The pressure and temperature at the beginning of compression of an air-standard Diesel cycle are 95 kPa and 300 K, respectively. At the end of the heat addition, the pressure is 7.2 MPa and the temperature is 2150 K. Determine:

a. the compression ratio, r.
b. the cutoff ratio, rc.
c. the thermal efficiency of the cycle, ?th (%).
d. the mean effective pressure, mep (kPa).

Answer 1

a) 23.19

b) 2.19

c) 0.597 ( 59.7%)

d) 975 KPa

Step-by-step explanation:

Solution:-

- We will determine the properties of the working fluid (Air) at each state value.

- We will seek help from air standard property tables ( A-22 ) and write down the following:

State 1:

P1 = 95 KPa , T1 = 300 K

u1 = 214.07 KJ/kg , vr1 = 621.2 , Pr1 = 1.386

- Using relations for isentropic compression we determine the reduced pressure value at state 2:

State 2:

P2 = P3 = 7200 KPa

`P_r_2 = P_r_1*((P_2)/(P_1) )\\\\P_r_2 = 1.386*((7200)/(95) ) = 105.04\\`

T2 = 979.6 K , vr2 = 26.793 , h2 = 1022.82 KJ/kg

State 3:

P3 = 7200 KPa , T3 = 2150 K

h3 = 2440.3 KJ/kg , vr3 = 2.175 , Pr1 = 1.386

- Using relations for isentropic expansion we determine the reduced volume value at state 4:

State 4:

`(v_4)/(v_3) = (v_1)/(v_2)*(v_2)/(v_3) = (v_r_1)/(v_r_2)*(T_2)/(T_3) \\\\(v_4)/(v_3) = (621.2)/(26.793)*(979.6)/(2150) = 10.56`

`v_r_4 = (v_4)/(v_3)*v_r_3 = 10.56*2.175\\\\v_r_4 = 22.98`

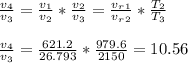
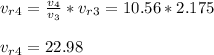
T4 = 1031 K , u4 = 785.75 KJ/kg

a) the compression ratio ( r )

- It is the ratio of volume decreased in the compression stroke ( State 1 -> state 2 ):

`r = (v_1)/(v_2) = (v_r_1)/(v_r_2) =(621.2)/(26.793)\\\\r = 23.19`

b) the cutoff ratio ( rc )

- It is the ratio of volume increased in the heat-addition process ( State 2 -> state 3 ):

`r_c = (v_3)/(v_2) = (T_3)/(T_2)\\\\r_c = (2150)/(979.6) = 2.19`

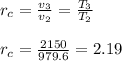
c) the thermal efficiency of the cycle ( nth )

- It is the ratio of total work-output from the cycle and the heat addition (Q23). The net work of the cycle is comprised of both heat addition(St2 - St3) and exhaust (St4 - St1 ). Hence, the work done by the cycle is:

`w_n_e_t = w_e - w_c\\\\w_n_e_t = (h_3 - h_2) - (u_4 - u_1 )\\\\w_n_e_t = (2440.3 - 1022.82) - (785.75 - 214.07 )\\\\w_n_e_t = 845.8 KJ/kg`

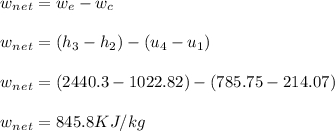
- The thermal efficiency of the cycle would be:

`n_t_h = (w_n_e_t)/(h_3 - h_2) = (845.8)/(2440.3-1022.82) \\\\n_t_h = (845.8)/(1417.48)\\\\n_t_h = 0.597`

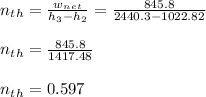
d) the mean effective pressure, mep

- It is the ratio of net work done by the cycle and the displaced volume of the compression stroke ( V1 - V2 ).

`mep = (w_n_e_t)/(V_1 - V_2) = (w_n_e_t)/(v_1( 1 - (v_2)/(v_1) )) = (w_n_e_t)/(v_1( 1 - (1)/(r) )) \\`

- We need to determine the specific volume of air at state 1. We will use ideal gas equation to determine.

`v_1 = (RT_1)/(P_1) = (0.287*300)/(95) \\\\v_1 = 0.9063 (m^3)/(kg)`

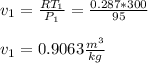
- Now we can use the calculated specific volume ( v1 ), compression ratio ( r ) and the net cycle work ( wnet ) to determine the ( mep ):

`mep = (845.8)/(0.9063*(1-(1)/(29.13)) ) \\\\mep= 975 KPa`