Question

Two objects moving with a speed v travel in opposite directions in a straight line. The objects stick together when they collide, and move with a speed of v/6 after the collision.Part A What is the ratio of the final kinetic energy of the system to the initial kinetic energy?KfKi=Part B What is the ratio of the mass of the more massive object to the mass of the less massive object?Mm=

Answer 1

A. K1/K2 = 36

B. M/m = 7/5

Step-by-step explanation:

Part A. In order to calculate the ratio of the final kinetic energy and the initial kinetic energy of the system, you first express the kinetic energy of the system before and after the collision.

Before the collision:

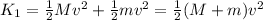`K_1=(1)/(2)Mv^2+(1)/(2)mv^2=(1)/(2)(M+m)v^2` (1)

After the collision:

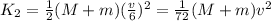`K_2=(1)/(2)(M+m)((v)/(6))^2=(1)/(72)(M+m)v^2` (2)

The quotient between K1 and K2 is given by:

`(K_1)/(K_2)=(1/2(M+m)v^2)/(1/72(M+m)v^2)=(1/2)/(1/72)=36`

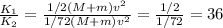
The quotient between the kinetic energy before and after the collision is K1/K2 = 36

Part B. To find the relation between the masses you use the momentum conservation law. The total momentum of the system before the collision and after the collision is given by:

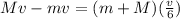`Mv-mv=(m+M)((v)/(6))` (3)

Where the minus sign in the first member of the equation means that the direction of the motion of both objects are opposite between them.

From the previous equation you can cancel the speed v and solve for M/m:

`(M-m)v=(m+M)((v)/(6))\\\\M-m=(1)/(6)(m+M)\\\\M-(1)/(6)M=(1)/(6)m+m\\\\(5)/(6)M=(7)/(6)m\\\\(M)/(m)=(7)/(5)`

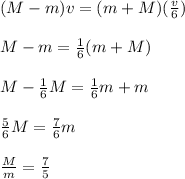
The ratio M/m is equal to 7/5