Question

I NEED HELP PLEASE, THANKS! :)

Answer 1

Option A

Explanation:

This is a great question!

The first thing we want to do here is to graph the system of " inequalities " -

`\begin{bmatrix}2x+9y\le \:100\\ 9x+y\le \:54\end{bmatrix}`

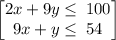
As x is ≥ 0, respectively y ≥ 0, it makes things a lot simpler, as it kind of restricts us to quadrant 1, but not entirely.

First change each inequality to " slope - intercept " form, as such -

`2x + 10y \leq 100,\\10y \leq 100 - 2x,\\y \leq - 1 / 5x + 10\\----------\\9x + y \leq 54,\\y \leq - 9x + 54`

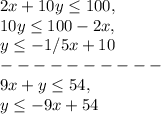
The graphed solutions would be in the attachment. I have colored the region with which the two intersect, and the fact that we are limited to quadrant 1. In this colored region there are 3 major points, ( 5, 9 ), ( 0, 10 ), and ( 6, 0 ). We have to determine which of these are are maximum points, as the minimum are the same. Substitute these values ( ( 5, 9 ), ( 0, 10 ), and ( 6, 0 ) ) into the equation f( x, y ) = 10x + 4y,

`f ( x, y ) = 10( 5 ) + 4( 9 ),\\f ( x, y ) = 86 -\\f ( x, y ) = 10( 0 ) + 4( 10 ),\\f ( x, y ) = 40 -\\f ( x, y ) = 10( 6 ) + 4( 0 ),\\f ( x, y ) = 60`

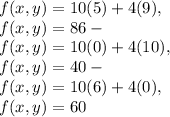
( 5, 9 ) resulted in the greatest amount, 86. That would make it our maximum point -

Solution = Option A