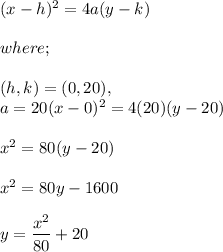Question

A satellite dish is being designed so that it can pick up radio waves coming from space. The satellite dish will be in the shape of a parabola and will be positioned above the ground such that its focus is 40 ft above the ground. Using the ground as the x-axis, where should the base of the satellite be positioned? Which equation best describes the equation of the satellite?

Answer 1

its ( 0,2 )

Step-by-step explanation:

not ( 0, 20) because it said it was wrong and then gave me the answer. I hope this helps. :))))

Answer 2

the base of the satellite should be positioned at (0,20)

the best model which describes the equation of the satellite is
`\mathbf{y = (x^2)/(80) + 20}`

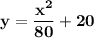
Step-by-step explanation:

From the information given:

A satellite dish is designed in such a way that it can pick up radio waves coming from the space.

This satellite dish is designed in the shape of a parabola.

Location of the satellite is situated above the ground

Focus of the satellite is 40 ft above the ground

Using the ground as the x - axis

The objective here is to determine where should the base of the satellite be positioned? &

Which equation best describes the equation of the satellite?

Using the ground as the x - axis;

Let say the x- axis start from the origin (0,0)

Then;

The Focus of the satellite which is 40 ft above the ground will be (0,40)

The position of the base of the satellite will be the vertex (h,k) which is at an equidistant position between the ground and the focus.

(h,k) = (0,20)

The model which best describes the equation of the satellite is as follows :

`(x - h)^2 = 4a(y - k) \\ \\ where ; \\ \\ (h,k) = (0,20) , \\ a = 20(x - 0)^2 = 4(20)(y - 20)\\ \\x^2 = 80( y - 20)\\ \\x^2= 80y - 1600\\ \\y = (x^2)/(80) + 20`