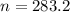Question

Suppose you wish to estimate a population mean correct to within 0.130.13 with a confidence level of 0.90. You do not know sigma squared σ2​, but you know that the observations will range in value between 36 and 44. Complete parts a and b.

Required:
a. Find the approximate sample size that will produce the desired accuracy of the estimate.
b. Calculate the approximate sample size, making the less conservative assumption that the range of the observations is equal to 6σ.

Answer 1

a

`n = 640 .4`

b

`n = 283.2`

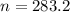
Explanation:

From the question we are told that

The population mean
`\= x = 0.90`

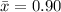
The confidence level
`\beta = 0.90`

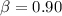
The range of the observation
`R = 44-36 = 8`

First we obtain the z-score of
`\beta` which is
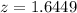`z = 1.6449` this is obtained from the z-table

Generally the standard deviation is mathematically represented as

`\sigma = (R)/(4)`

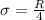
substituting values

`\sigma = (8)/(4)`

`\sigma = 2`

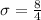
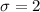
Now the sample size is mathematically represented as

`n = [ z * (\sigma)/(\= x) ]^2`

substituting values

`n = [ 1.6449 * (2)/(0.13) ]^2`

`n = 640 .4`

When the range is equal to
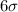`6 \sigma` it implies that

`R = 6 \sigma = 8`

=>
`\sigma = (8)/(6)`

=>
`\sigma = 1.333`

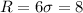
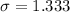
So the sample size is mathematically represented as

`n = [ 1.6449 * (1.33)/(0.13) ]^2`

`n = 283.2`