Question

A boat, which moves at 13 miles per hour in water without a current, goes 80 miles upstream and 80 miles back again in 13 hours. Find the speed of the current to the nearest tenth.

Answer 1

Speed of current is 3 miles per hour.

Explanation:

Speed of boat without current, u = 13 miles/hr

Let speed of current = v miles/hr

Speed upstream = (13 - v) miles/hr

Speed downstream = (13 + v) miles/hr

Distance traveled upstream,
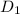`D_1` = 80 miles

Distance traveled downstream,
`D_2` = 80 miles

Total time taken, T (
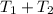`T_1+T_2`) = 13 hours

Formula for Total Time taken:

`Time= (Distance)/(Speed)`

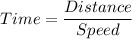
Time taken in Upstream:

`T_1 = (80)/(13-v)\ hours`

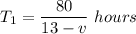
Time taken in Downstream:

`T_2 = (80)/(13+v)\ hours`

`T = T_1+T_2 = 13\ hours\\\Rightarrow 13 = (80)/(13-v)+(80)/(13+v)\\\Rightarrow 13 = 80((13+v+13-v)/(13^2-v^2))\\\Rightarrow 13^2-v^2 = (80(26))/(13)\\\Rightarrow 169-v^2 = 80* 2\\\Rightarrow v^2 = 169-160 = 9\\\Rightarrow v = 3\ miles/hr`

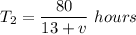
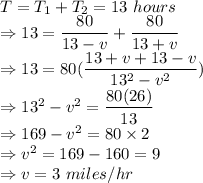
So, speed of current is 3 miles/hr