Question

PLEASE HELP MEEEE HURRRY!!! :)

Answer 1

Option D

Explanation:

We are given the following equations -

`\begin{bmatrix}-5x-12y-43z=-136\\ -4x-14y-52z=-146\\ 21x+72y+267z=756\end{bmatrix}`

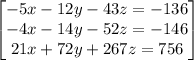
It would be best to solve this equation in matrix form. Write down the coefficients of each terms, and reduce to " row echelon form " -

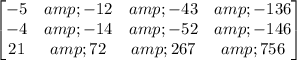`\begin{bmatrix}-5&-12&-43&-136\\ -4&-14&-52&-146\\ 21&72&267&756\end{bmatrix}` First, I swapped the first and third rows.

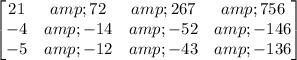`\begin{bmatrix}21&72&267&756\\ -4&-14&-52&-146\\ -5&-12&-43&-136\end{bmatrix}` Leading coefficient of row 2 canceled.

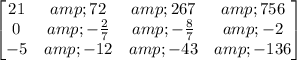`\begin{bmatrix}21&72&267&756\\ 0&-(2)/(7)&-(8)/(7)&-2\\ -5&-12&-43&-136\end{bmatrix}` The start value of row 3 was canceled.

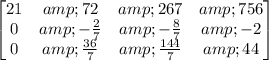`\begin{bmatrix}21&72&267&756\\ 0&-(2)/(7)&-(8)/(7)&-2\\ 0&(36)/(7)&(144)/(7)&44\end{bmatrix}` Matrix rows 2 and 3 were swapped.

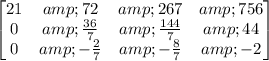`\begin{bmatrix}21&72&267&756\\ 0&(36)/(7)&(144)/(7)&44\\ 0&-(2)/(7)&-(8)/(7)&-2\end{bmatrix}` Leading coefficient in row 3 was canceled.

`\begin{bmatrix}21&72&267&756\\ 0&(36)/(7)&(144)/(7)&44\\ 0&0&0&(4)/(9)\end{bmatrix}`

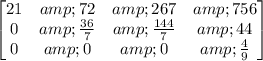
And at this point, I came to the conclusion that this system of equations had no solutions, considering it reduced to this -

`\begin{bmatrix}1&0&-1&0\\ 0&1&4&0\\ 0&0&0&1\end{bmatrix}`

The positioning of the zeros indicated that there was no solution!

Hope that helps!