Question

A spring attached to the ceiling is stretched one foot by a four pound weight. The mass is set in motion by pulling down 2 feet and then released in a medium with a damping force numerically equal to the velocity.

a. Find the Hook's law spring constant k.
b. Find its natural frequency ω.
c. Form a differential equation for the position x(t) of the mass.
d. Determine the solution for the position (in alternate form).
e. Find the times at which the mass passes the equilibrium second time heading up.

Answer 1

Given that,

Weight = 4 pound

`W=4\ lb`

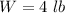
Stretch = 2 feet

Let the force be F.

The elongation of the spring after the mass attached is

`x=2-1=1\ feet`

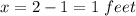
(a). We need to calculate the value of spring constant

Using Hooke's law

`F=kx`

`k=(F)/(x)`

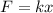
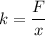
Where, F = force

k = spring constant

x = elongation

Put the value into the formula

`k=(4)/(1)`

`k=4`

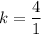
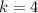
(b). We need to calculate the mass

Using the formula

`F=mg`

`m=(F)/(g)`

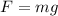
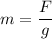
Where, F = force

g = acceleration due to gravity

Put the value into the formula

`m=(4)/(32)`

`m=(1)/(8)\ lb`

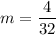
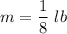
We need to calculate the natural frequency

Using formula of natural frequency

`\omega=\sqrt{(k)/(m)}`

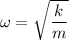
Where, k = spring constant

m = mass

Put the value into the formula

`\omega=\sqrt{(4)/((1)/(8))}`

`\omega=√(32)`

`\omega=4√(2)`

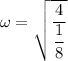
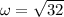
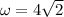
(c). We need to write the differential equation

Using differential equation

`m(d^2x)/(dt^2)+kx=0`

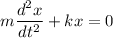
Put the value in the equation

`(1)/(8)(d^2x)/(dt^2)+4x=0`

`(d^2x)/(dt^2)+32x=0`

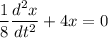
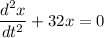
(d). We need to find the solution for the position

Using auxiliary equation

`m^2+32=0`

`m=\pm i√(32)`

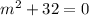
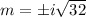
We know that,

The general equation is

`x(t)=A\cos(√(32t))+B\sin(√(32t))`

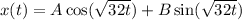
Using initial conditions

(I).
`x(0)=2`

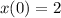
Then,
`x(0)=A\cos(√(32*0))+B\sin(√(32*0))`

Put the value in equation

`2=A+0`

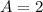`A=2`.....(I)

Now, on differentiating of general equation

`x'(t)=-√(32)A\sin(√(32t))+√(32)B\cos(√(32t))`

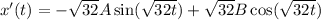
Using condition

(II).
`x'(0)=0`

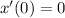
Then,
`x'(0)=-√(32)A\sin(√(32*0))+√(32)B\cos(√(32*0))`

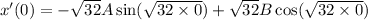
Put the value in the equation

`0=0+√(32)B`

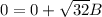
So, B = 0

Now, put the value in general equation from equation (I) and (II)

So, The general solution is

`x(t)=2\cos√(32t)`

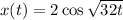
(e). We need to calculate the time

Using formula of time

`T=(2\pi)/(\omega)`

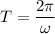
Put the value into the formula

`T=(2\pi)/(4√(2))`

`T=1.11\ sec`

Hence, (a). The value of spring constant is 4.

(b). The natural frequency is 4√2.

(c). The differential equation is
`(d^2x)/(dt^2)+32x=0`

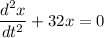
(d). The solution for the position is
`x(t)=2\cos√(32t)`

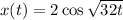
(e). The time period is 1.11 sec.