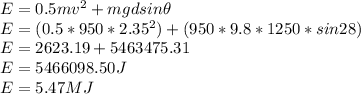Question

A loaded ore car has a mass of 950 kg and rolls on rails with negligible friction. It starts from rest and is pulled up a mine shaft by a cable connected to a winch. The shaft is inclined at 28.0° above the horizontal. The car accelerates uniformly to a speed of 2.35 m/s in 14.0 s and then continues at constant speed.(A) What power must the winch motor provide when the car is moving at constant speed? kW(B) What maximum power must the motor provide? kW(C) What total energy transfers out of the motor by work by the time the car moves off the end of the track, which is of length 1,250 m?

Answer 1

a) P = 10.27 kW

b) Pmax = 10.65 kW

c) E = 5.47 MJ

Step-by-step explanation:

Mass of the loaded car, m = 950 kg

Angle of inclination of the shaft, θ = 28°

Acceleration due to gravity, g = 9.8 m/s²

The speed of the car, v = 2.35 m/s

Change in time, t = 14.0 s

a) The power that must be provided by the winch motor when the car is moving at constant speed.

P = Fv

The force exerted by the motor, F = mg sinθ

P = mgv sinθ

P = 950 * 9.8 *2.35* sin28°

P = 10,271.3 W

P = 10.27 kW

b) Maximum power that the motor must provide:

`P = mv(dv)/(dt) + mgvsin \theta\\dv/dt = (2.35 - 0)/(14) \\dv/dt = 0.168 m/s^2\\P = (950*2.35*0.168) + (950*9.8*2.35* sin28)\\P = 374.74 + 10271.3\\P = 10646.04 W\\10.65 kW`

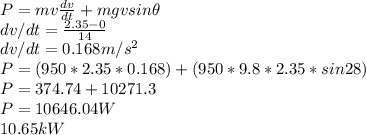
c) Total energy transferred:

Length of the track, d = 1250 m

`E = 0.5 mv^2 + mgd sin \theta\\E = (0.5 * 950 * 2.35^2) + (950 * 9.8 * 1250 * sin 28)\\E = 2623.19 + 5463475.31\\E = 5466098.50 J\\E = 5.47 MJ`