Think about this. If we were to align the coefficients with their solutions to form this matrix, it would be the following -
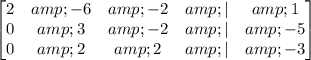
Now this is one way to assign the coefficients. As you can see, 2, - 6, - 2 are present as the coefficients for the first row. Similarly 0, 3, - 2 are present as the coefficients for the second row - ( as one term is missing from this row, it is replaced with a " 0 " ). The same applies for the third row. The end values of the system of equation is present as the last column.
The options are assigned in a manner with which the coefficients and variables are present in two columns, while the end values of the system of equation given, is present as the last column. Knowing the arrangement of both the coefficients and the end values of the system of equation, all we have to do is add these " variables " as one column -
Solution = Option B