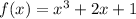Question

Use Newton’s Method to approximate the zero(s) of the function. Continue the iterations until two successive approximations differ by less than 0.001. Then find the zero(s) using a graphing utility and compare the results. f(x) = x 3 + 2x + 1f (x) = x 3 + 2 x+1

Answer 1

`S=\{-0.45339,...\}`

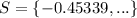
Explanation:

Hi!

Greetings

1) Firstly let's graph the function using an utility (Check below). That's how we're going to pick our
`x_1`

2) Let's now use the algorithm. Since we've seen the graph let's now choose one approximation to start with:

`x_(n+1)=x-(f(x))/(f'(x))\\x_(1)=-0.4\\x_(2)=(-0.4)-((-0.4)^(3)+2(-0.4)+1)/(3(-0.4)^2+2) \approx -0.45483\\x_(3)=(-0.45483)-((-0.45483)^(3)+2(-0.45483)+1)/(3(-0.45483 )^2+2)\approx -0.45339\\x_(4)=(-0.45339)-((-0.45339)^(3)+2(-0.45339)+1)/(3(-0.45339 )^2+2)\approx -0.45339\\`

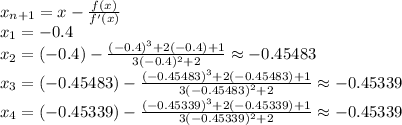
Since the approximations started to repeat, then it is safe to say that

this approximation is one of the roots for the function
`f(x)=x^(3)+2x+1`