Question

The equation of a linear function in point-slope form is y – y1 = m(x – x1). Harold correctly wrote the equation y = 3(x – 7) using a point and the slope. Which point did Harold use?

Answer 1

(7,0)

Explanation:

Answer 2

Point used by Harold was:

(7, 0)

Explanation:

Given that

Equation of linear function used by Harold:

`y = 3(x - 7)`

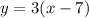
We know that linear equation in point slope form can be represented as:

`y - y_1 = m(x - x_1)`

Where
`(x_1,y_1)` are the coordinates of a given point.

`m` is the slope of line.

Formula for Slope, m is given as:

`m = (y_2-y_1)/(x_2-x_1)`

Where
`(x_1,y_1)` and
`(x_2,y_2)` are the two points on the line.

If slope and a point with coordinates
`(x_1,y_1)` is know, the equation of a line can be represented in linear form as:

`y - y_1 = m(x - x_1)` ....... (1)

Now, the given equation is:

`y = 3(x - 7)`

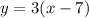
Re-writing the equation with a slight modification:

`y-0 = 3(x - 7)`

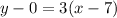
Now, comparing the above equation with equation (1):

We get that:

`x_1=7\\y_1=0`

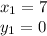
So, the point used by Harold is (7, 0).