Answer:
95% of confidence interval for the Population
( 6.1386 , 6.8614)
Explanation:
Step( i ):-
Given random sample size 'n' =85
Mean of the sample size x⁻ = 6.5 years
Standard deviation of Population = 1.7 years
Level of significance = 0.95 or 0.05
Step(ii):-
95% of confidence interval for the Population is determined by
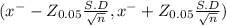
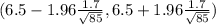
( 6.5 - 0.3614 , 6.5 + 0.3614 )
( 6.1386 , 6.8614)
Conclusion:-
95% of confidence interval for the Population
( 6.1386 , 6.8614)