Answer:
8.7 m/s^2
82.15°
Step-by-step explanation:
Given:-
- The initial speed of the car, vi = 25 m/s
- The radius of track, r = 129 m
- Car makes a circular " quarter turn "
- The constant tangential acceleration, at = 1.2 m/s^2
Solution:-
- We will solve the problem using rotational kinematics. Determine the initial angular velocity of car ( wi ) as follows:
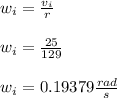
- Now use the constant tangential acceleration ( at ) and determine the constant angular acceleration ( α ) for the rotational motion as follows:
at = r*α
α = ( 1.2 / 129 )
α = 0.00930 rad/s^2
- We know that the angular displacement from the initial entry to the exit of the turn is quarter of a turn. The angular displacement would be ( θ = π/2 ).
- Now we will use the third rotational kinematic equation of motion to determine the angular velocity at the exit of the turn (wf) as follows:
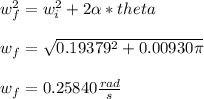
- We will use the evaluated final velocity ( wf ) and determine the corresponding velocity ( vf ) as follows:
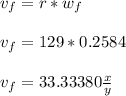
- Now use the formulation to determine the centripetal acceleration ( ac ) at this point as follows:
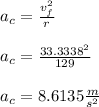
- To determine the magnitude of acceleration we will use find the resultant of the constant tangential acceleration ( at ) and the calculated centripetal acceleration at the exit of turn ( ac ) as follows:
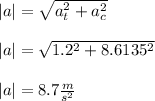
- To determine the angle between the velocity vector and the acceleration vector. We need to recall that the velocity vector only has one component and always tangential to the curved path. Hence, the velocity vector is parallel to the tangential acceleration vector ( at ). We can use the tangential acceleration ( at ) component of acceleration ( a ) and the centripetal acceleration ( ac ) component of the acceleration and apply trigonometric ratio as follows:
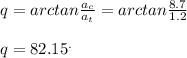
Answer: The angle ( q ) between acceleration vector ( a ) and the velocity vector ( v ) at the exit of the turn is 82.15° .