Question

What is the probability of selecting a male from a group of 4

males and 8 females?
1
A 1/3
B 1/2
С 2/3
D 4/5

Answer 1

`P(Male) = (1)/(3)`

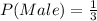
Explanation:

Given

`Male = 4`

`Female = 8`

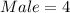
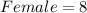
Required

Probability of selecting a male

First, we need to get the total population;

`Total = Male + Female`

`Total = 4 + 8`

`Total = 12`

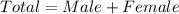
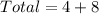
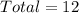
Let P(Male) represent Probability of Male

Let n(Male) represent number of Male

`P(Male) = (n(Male))/(Total)`

`P(Male) = (4)/(12)`

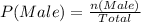
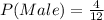
Simplify fraction by dividing the numerator and denominator by 4

`P(Male) = (1)/(3)`

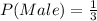
Hence, the probability of selecting a male is 1/3