Question

Flip a coin 10 times and record the observed number of heads and tails. For example, with 10 flips one might get 6 heads and 4 tails. Now, flip the coin another 20 times (so 30 times in total) and again, record the observed number of heads and tails. Finally, flip the coin another 70 times (so 100 times in total) and record your results again.

We would expect that the distribution of heads and tails to be 50/50. How far away from 50/50 are you for each of your three samples? Reflect upon why might this happen?

Answer 1

The greater the sample size the better is the estimation. A large sample leads to a more accurate result.

Explanation:

Consider the table representing the number of heads and tails for all the number of tosses:

Number of tosses n (HEADS) n (TAILS) Ratio

10 3 7 3 : 7

30 14 16 7 : 8

100 60 40 3 : 2

Compute probability of heads for the tosses as follows:

• n = 10 tosses

`P(\text{HEADS})=(3)/(10)=0.30`

The probability of heads in case of 10 tosses of a coin is -0.20 away from 50/50.

• n = 30 tosses

`P(\text{HEADS})=(14)/(30)=0.467`

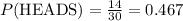
The probability of heads in case of 30 tosses of a coin is -0.033 away from 50/50.

• n = 100 tosses

`P(\text{HEADS})=(60)/(100)=0.60`

The probability of heads in case of 100 tosses of a coin is 0.10 away from 50/50.

As it can be seen from the above explanation, that as the sample size is increasing the distance between the expected and observed proportion is decreasing.

This happens because, the greater the sample size the better is the estimation. A large sample leads to a more accurate result.