Answer:
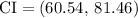
Therefore, we are 95% confident that actual mean savings for a televisit to the doctor is within the interval of ($60.54 to $81.46)
Explanation:
Let us find out the mean savings for a televisit to the doctor from the given data.
Using Excel,
=AVERAGE(number1, number2,....)
The mean is found to be

Let us find out the standard deviation of savings for a televisit to the doctor from the given data.
Using Excel,
=STDEV(number1, number2,....)
The standard deviation is found to be
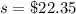
The confidence interval is given by
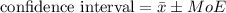
Where the margin of error is given by
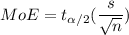
Where n is the sample of 20 online doctor visits, s is the sample standard deviation and
 is the t-score corresponding to a 95% confidence level.
is the t-score corresponding to a 95% confidence level.
The t-score is given by is
Significance level = α = 1 - 0.95 = 0.05/2 = 0.025
Degree of freedom = n - 1 = 20 - 1 = 19
From the t-table at α = 0.025 and DoF = 19
t-score = 2.093
So, the margin of error is
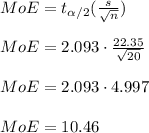
So the required 95% confidence interval is
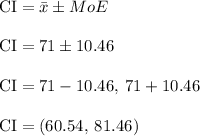
Therefore, we are 95% confident that actual mean savings for a televisit to the doctor is within the interval of ($60.54 to $81.46)