Question

Three populations have proportions 0.1, 0.3, and 0.5. We select random samples of the size n from these populations. Only two of the distributions of the sample proportions are normally distributed. Choose all possible values of n.

a. 10
b. 100
c. 50
d. 40
e. 20

Answer 1

(1) A Normal approximation to binomial can be applied for population 1, if n = 100.

(2) A Normal approximation to binomial can be applied for population 2, if n = 100, 50 and 40.

(3) A Normal approximation to binomial can be applied for population 2, if n = 100, 50, 40 and 20.

Explanation:

Consider a random variable X following a Binomial distribution with parameters n and p.

If the sample selected is too large and the probability of success is close to 0.50 a Normal approximation to binomial can be applied to approximate the distribution of X if the following conditions are satisfied:

• np ≥ 10
• n(1 - p) ≥ 10

The three populations has the following proportions:

p₁ = 0.10

p₂ = 0.30

p₃ = 0.50

(1)

Check the Normal approximation conditions for population 1, for all the provided n as follows:

`n_(a)p_(1)=10* 0.10=1<10\\\\n_(b)p_(1)=100* 0.10=10=10\\\\n_(c)p_(1)=50* 0.10=5<10\\\\n_(d)p_(1)=40* 0.10=4<10\\\\n_(e)p_(1)=20* 0.10=2<10`

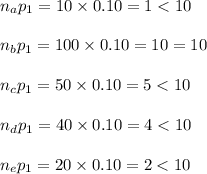
Thus, a Normal approximation to binomial can be applied for population 1, if n = 100.

(2)

Check the Normal approximation conditions for population 2, for all the provided n as follows:

`n_(a)p_(1)=10* 0.30=3<10\\\\n_(b)p_(1)=100* 0.30=30>10\\\\n_(c)p_(1)=50* 0.30=15>10\\\\n_(d)p_(1)=40* 0.10=12>10\\\\n_(e)p_(1)=20* 0.10=6<10`

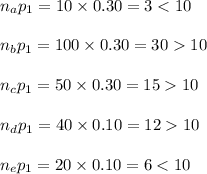
Thus, a Normal approximation to binomial can be applied for population 2, if n = 100, 50 and 40.

(3)

Check the Normal approximation conditions for population 3, for all the provided n as follows:

`n_(a)p_(1)=10* 0.50=5<10\\\\n_(b)p_(1)=100* 0.50=50>10\\\\n_(c)p_(1)=50* 0.50=25>10\\\\n_(d)p_(1)=40* 0.50=20>10\\\\n_(e)p_(1)=20* 0.10=10=10`

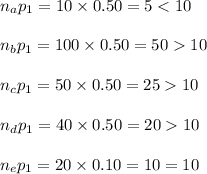
Thus, a Normal approximation to binomial can be applied for population 2, if n = 100, 50, 40 and 20.