Question

+23PTS PROMISE ! PDF TWO SAT QUESTIONS w/ explanation. Graph question -_- Correct Answer #37: 576 Correct Answer #38: 0.8 PLEASE MAKE THE EXPLANATION MORE CLEAR! THANK YOU

Answer 1

i’m just taking the points. sorry

Answer 2

Step-by-step explanation:

#37: The data is per milliliter, so to find out how much pen*cillin is present for TEN milliliters, multiply the value by 10. So, after 5 minutes, there were 152 micr*grams of penic*llin per milliliter in the kidn*ys, which means 1520 (152 x 10) micr*grams per TEN milliliters of bl*od. Now, for step 2 we need to go to row three and calculate the amount of penic*llin (in micr*grams, no conversion necessary) per EIGHT milliliters of bl*od, NOT TEN. Therefore, we are going to multiply the per milliliter value by EIGHT. 118 x 8 = 944. To answer the question we need to find the positive difference (the questions asks for how much MORE, NOT LESS) between 1520 and 944. This is 576 (1520 - 944 = 576).

#38: to get an the most accurate reading for variable P, you can use any data in the table except for row one, because this is immediately after injection, the full amount of penic*llin given in the d*se.

Formula for depreciation of penic*llin in body after inj*ction (measured in intervals of 5 mintues): P(t) = 200b^(t/5)

See, if we solve for "b" using any of the rows after 1 we will get a very similar answer and when rounded to the nearest tenth, they will all equal 0.8.

**the "P(t)" is the same as function of x which is equivalent to the output (y value) in a table.

Row Two

`P(5) = 200b^(5/5)\\152 = 200b^1\\152 = 200b\\152/200 = b\\b = 0.76 = 0.8\\` (nearest tenth)

Row Three

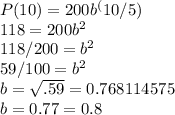`P(10) = 200b^(10/5)\\118 = 200b^2\\118/200 = b^2\\59/100 = b^2\\b = √(.59) = 0.768114575\\b = 0.77 = 0.8` (nearest tenth)

Row Four

`P(15) = 200b^(15/5)\\93 = 200b^3\\93/200 = b^3\\0.465 = b^3\\b = \sqrt[3]{0.465} = 0.774731089\\b = 0.77 = 0.8`(nearest tenth)

Row Five

`P(20) = 200b^(20/5)\\74 = 200b^4\\74/200 = b^4\\37/100 = b^4\\b^4 = .37\\b = \sqrt[4]{0.37} = 0.77992067098508\\b = 0.78 = 0.8` (nearest tenth)