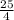Question

A tourist can bicycle 28 miles in the same time as he can walk 8 miles. If he can ride 10 mph faster than he can walk, how much time (in hr) should he allow to walk a 25-mile trail? (Hint: How fast can he walk?) ________ hr. (enter a fraction)

Answer 1

The answer is
`(25)/(4)`

Explanation:

Velocity formula:

`v = (d)/(t)`

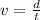
In which v is the velocity, d is the distance, and t is the time.

A tourist can bicycle 28 miles in the same time as he can walk 8 miles. He can ride 10 mph faster than he can walk:

This means that:

`v = (8)/(t)`

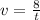
And

`v + 10 = (28)/(t)`

`(v + 10)t = 28`

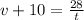
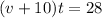
From the first equation:

`vt = 8`

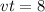
So

`vt + 10 = 28`

`8 + 10t = 28`

`10t = 20`

`t = (20)/(10)`

`t = 2`

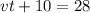
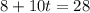
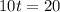
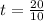
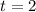
He walks 8 miles in two hours, so:

`v = (8)/(2) = 4`

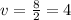
4 miles per hour.

How much time (in hr) should he allow to walk a 25-mile trail?

This is t when
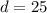`d = 25`. So

`v = (d)/(t)`

`4 = (25)/(t)`

`4t = 25`

`t = (25)/(4)`

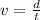
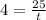
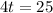
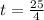
The answer is
`(25)/(4)`