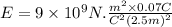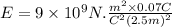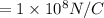Question

One of the hazards facing humans in space is space radiation: high-energy charged particles emitted by the sun. during a solar flare, the intensity of this radiation can reach lethal levels. one proposed method of protection for astronauts on the surface of the moon or mars is an array of large, electrically charged spheres placed high above areas where people live and work. the spheres would produce a strong electric field e⃗ to deflect the charged particles that make up space radiation. the spheres would be similar in construction to a mylar balloon, with a thin, electrically conducting layer on the outside surface on which a net positive or negative charge would be placed. a typical sphere might be 5 m in diameter. suppose that to repel electrons in the radiation from a solar flare, each sphere must produce an electric field e⃗ of magnitude 1 × 106 n/c at 25 m from the center of the sphere. what is the magnitude of e just outside the surface of such a sphere

Answer 1

`1* 10^(8) N/C`

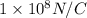
Step-by-step explanation:

According to the gauss law

As we know that

Electric field is

`E = -k(q)/(r^2)`

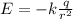
where,

k = column constant =
`9 * 10 ^(9)\ N. (m^2)/(c^2)`

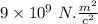
q = charge

r = distance from the sphere center

For computing the magnitude of e first we have to need to find out the charge outside of sphere which is

`q = -(Er^2)/(k)`

`q = -(1 * 10^(6) (N)/(C) (25m)^2)/(9 * 10 ^(9)\ N. (m^2)/(c^2))`

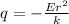
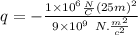
q = -0.07 C

Now we have to find the electric field

`E = k(q)/(r^2)`

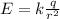
The r is 2.5m but in question it is given 5m

So,

Electric field is

`E = 9 * 10^(9) N . (m^2 * 0.07 C)/(C^2 (2.5 m)^2)`

`E = 9 * 10^(9) N. \frac{m^2 * 0.07 C} {C^2 (2.5m)^2}`

`= 1* 10^(8) N/C`