Question

Three solid shapes A,B and C The surface area of shape A is 9cm² The surface area of shape B is 16cm² The ratio of the volume of shape B to the volume of shape C is 27 : 125 Work out the ratio of the height of shape A to the height of shape C

Answer 1

9:20

Explanation:

Given:

Surface area of shape A = 9 cm²

Surface Area of shape B = 16 cm²

Ratio of volume of shape A to B = 27:125

Required:

Find the ratio of the height of shape A to the height of shape C.

Ratio of surface area (A:B)² = ratio of linear measures (A:B)

Thus,

(A:B)² = (A:B)

(A/B)² = (A/B)

`((A)/(B))^2= ((9)/(16))`

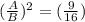
Take the square root of both sides:

`(\sqrt{(A)/(B)})^2 = (\sqrt{(9)/(16)})`

`(A)/(B) = (3)/(4)`

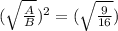
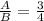
Ratio of volume of shape B to C = 27:125

Thus,

(B:C)³ = 27:125

`((B)/(C))^3= ((27)/(125))`

Take the cube root of both sides:

`(3\sqrt{(B)/(C)})^3 = (3\sqrt{(27)/(125)})`

`(B)/(C) = (3)/(5)`

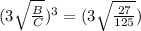
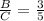
Therefore, ratio of lengths A:B:C =

3:4:C

A:3:5

To make them equivalent, we have:

9:12:C

A:4:20

Therefore, the ratio of the height of shape A to the height of shape C =

9:20