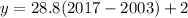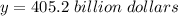Answer:
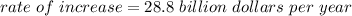
model:
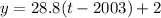
profit in year 2017:
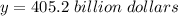
Explanation:
The sales increased from 2 billion dollars to 146 billion dollars in five years, so to find the increase in billion dollars per year, we just need to divide the increase by the amount of time:
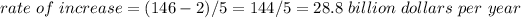
To construct a model for these sales, we can use the year 2003 as the initial point of a linear equation:
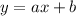
the variable y will represent the profit in billion dollars, the variable x will represent our time, so we can use (t - 2003) in its place to represent the number of years since 2003 (t is the year we want to calculate), the constant 'a' will be our rate of 28.8, and the constant 'b' is the inicial value for the year 2003, that is, 2 (billions). So we have:
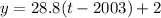
In the year 2017, we would have: