Answer:
Step 4
Explanation:
The table is given below

Tasha wants to find the value of
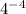 .
.
Her steps are:
Step 1: Find a pattern in the table.
The pattern is to divide the previous value by 4 when the exponent decreases by 1.
Step 2: Find the value of
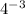 .
.
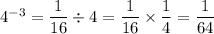
Step 3: Find the value of
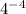 .
.
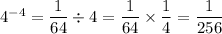
Step 4: Rewrite the value for
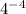 .
.
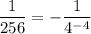
Tasha made her first error in Step 4. The correct step is:
