Answer:
Since the speed can't be negative it was 60 km/h for the first stage and 80 km/h on the second stage, averaging 70 km/h for the whole course.
Explanation:
The speed of the truck for the first stage of the route is "x" km/h, while on the second one it raises to "x + 20" km/h. The time it takes to complete each stage is shown below:

The sum of these times must be equal to the total time of the trip, therefore:
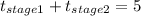
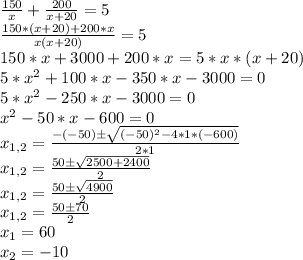
Since the speed can't be negative it was 60 km/h for the first stage and 80 km/h on the second stage, averaging 70 km/h for the whole course.