Answer:
The t-score that should be used to find the 90% confidence interval is 1.729.
Explanation:
The (1 - α)% confidence interval population mean, when the population standard deviation is not known is:
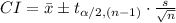
The information provided is:
n = 20
α = 0.10
The degrees of freedom of t-statistic will be:
df = n - 1
= 20 - 1
= 19
Compute the critical value of t as follows:
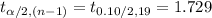
*Use a t-table.
Thus, the t-score that should be used to find the 90% confidence interval is 1.729.