Answer:
a) 27
b) 15
Explanation:
An uniform probability is a case of probability in which each outcome is equally as likely.
For this situation, we have a lower limit of the distribution that we call a and an upper limit that we call b.
The mean of the uniform distribution is:
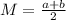
The variance of the uniform distribution is given by:
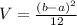
The standard deviation is the square root of the variance.
They can be said to follow a Uniform distribution from 1 to 53
This means that
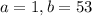
a. The mean of this distribution is
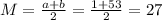
b. The standard deviation is: