Question

In a random sample of 600 cars making a right turn at a certain intersection, 157 pulled into the wrong lane. Test the hypothesis that actually 30% of all drivers make this mistake at the given intersection. Use the level of significance.a) α = 0.05

b) α = 0.01

Answer 1

a)

The statistic value |Z| = 2.053 > 1.96 at 0.05 Level of significance

Null hypothesis is rejected

Alternative hypothesis is Accepted

Actually 30% of all drivers make not this mistake at the given intersection

b)

The test statistic value |Z| = 2.053 >2.576 at 0.01 Level of significance

Null hypothesis is Accepted

Actually 30% of all drivers make this mistake at the given intersection

Explanation:

Step(i):-

Given Population proportion = 30% or 0.30

Given data In a random sample of 600 cars making a right turn at a certain intersection, 157 pulled into the wrong lane

sample proportion

`p^(-) = (x)/(n) = (157)/(600) = 0.2616`

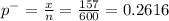
Null hypothesis:- H₀: p = 0.30

Alternative hypothesis : H₁:p≠0.30

Step(ii):-

a)

Test statistic

`Z = \frac{p^(-)-P }{\sqrt{(p(1-p))/(n) } }`

`Z = \frac{0.2616-0.30 }{\sqrt{(0.30(1-0.30))/(600) } }`

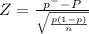
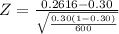
Z = -2.053

|Z| = |-2.053| = 2.053

Level of significance = 0.05

Z₀.₀₅ = 1.96

The calculated value |Z| = 2.053 > 1.96 at 0.05 Level of significance

Null hypothesis is rejected

Alternative hypothesis is Accepted

Conclusion:-

Actually 30% of all drivers make not this mistake at the given intersection

b)

Given level of significance = 0.01

Z₀.₀₁ = 2.576

The calculated value |Z| = 2.053 >2.576 at 0.01 Level of significance

Null hypothesis is Accepted

Actually 30% of all drivers make this mistake at the given intersection