Question

Rosetta wants to estimate the percentage of people who rent their home. She surveys 250 individuals and finds that 48 rent their home. Use a calculator to find the confidence interval for the population proportion with a 90% confidence level. 0.10 0.05 0.025 0.01 0.005 1.282 1.645 1.960 2.326 2.576

Answer 1

`0.192 - 1.645\sqrt{(0.192(1-0.192))/(250)}=0.151`

`0.192 + 1.645\sqrt{(0.192(1-0.192))/(250)}=0.233`

Explanation:

Information given

`X= 48` number of people who rent their home

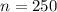`n= 250` represent the sample size

`\hat p =(48)/(250)= 0.192` represent the proportion of people who rent their home

In order to find the critical value we need to take in count that we are finding the interval for a proportion, so on this case we need to use the z distribution. Since our interval is at 90% of confidence, our significance level would be given by
`\alpha=1-0.90=0.1` and
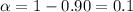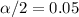`\alpha/2 =0.05`. And the critical value would be given by:

`z_(\alpha/2)=\pm 1.645`

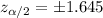
The confidence interval for the mean is given by the following formula:

`\hat p \pm z_(\alpha/2)\sqrt{(\hat p (1-\hat p))/(n)}`

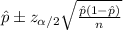
If we replace the values obtained we got:

`0.192 - 1.645\sqrt{(0.192(1-0.192))/(250)}=0.151`

`0.192 + 1.645\sqrt{(0.192(1-0.192))/(250)}=0.233`