Question

The mean and standard deviation of a random sample of n measurements are equal to 34.5 and 3.4, respectively.A. Find a 95 % confidence interval for μ if n=49.B. Find a 95% confidence interval for μ if n=196.C. Find the widths of the confidence intervals found in parts a and b.D. What is the effect on the width of a confidence interval of quadrupling the sample size while holding the confidence coefficient fixed?1. Quadrupling the sample size while holding the confidence coefficient fixed decreases the width of the confidence interval by a factor of 4.2. Quadrupling the sample size while holding the confidence coefficient fixed increases the width of the confidence interval by a factor of 2.3. Quadrupling the sample size while holding the confidence coefficient fixed increases the width of the on confidence interval by a factor of 4.4. Quadrupling the sample size while holding the confidence coefficient fixed does not affect the width of the confidence interval.5. Quadrupling the sample size while holding the confidence coefficient fixed decreases the width of the confidence interval by a factor of 2.

Answer 1

a. The 95% confidence interval for the mean is (33.52, 35.48).

b. The 95% confidence interval for the mean is (34.02, 34.98).

c. n=49 ⇒ Width = 1.95

n=196 ⇒ Width = 0.96

Note: it should be a factor of 2 between the widths, but the different degrees of freedom affects the critical value for each interval, as the sample size is different. It the population standard deviation had been used, the factor would have been exactly 2.

d. 5. Quadrupling the sample size while holding the confidence coefficient fixed decreases the width of the confidence interval by a factor of 2.

Explanation:

a. We have to calculate a 95% confidence interval for the mean.

The population standard deviation is not known, so we have to estimate it from the sample standard deviation and use a t-students distribution to calculate the critical value.

The sample mean is M=34.5.

The sample size is N=49.

When σ is not known, s divided by the square root of N is used as an estimate of σM:

`s_M=(s)/(√(N))=(3.4)/(√(49))=(3.4)/(7)=0.486`

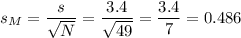
The degrees of freedom for this sample size are:

`df=n-1=49-1=48`

The t-value for a 95% confidence interval and 48 degrees of freedom is t=2.011.

The margin of error (MOE) can be calculated as:

`MOE=t\cdot s_M=2.011 \cdot 0.486=0.98`

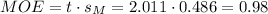
Then, the lower and upper bounds of the confidence interval are:

`LL=M-t \cdot s_M = 34.5-0.98=33.52\\\\UL=M+t \cdot s_M = 34.5+0.98=35.48`

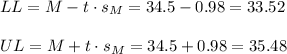
The 95% confidence interval for the mean is (33.52, 35.48).

b. We have to calculate a 95% confidence interval for the mean.

When σ is not known, s divided by the square root of N is used as an estimate of σM:

`s_M=(s)/(√(N))=(3.4)/(√(196))=(3.4)/(14)=0.243`

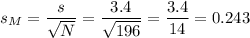
The degrees of freedom for this sample size are:

`df=n-1=196-1=195`

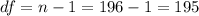
The t-value for a 95% confidence interval and 195 degrees of freedom is t=1.972.

The margin of error (MOE) can be calculated as:

`MOE=t\cdot s_M=1.972 \cdot 0.243=0.48`

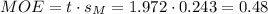
Then, the lower and upper bounds of the confidence interval are:

`LL=M-t \cdot s_M = 34.5-0.48=34.02\\\\UL=M+t \cdot s_M = 34.5+0.48=34.98`

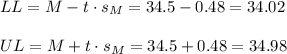
The 95% confidence interval for the mean is (34.02, 34.98).

c. The width of the intervals is:

`n=49\rightarrow UL-LL=33.52-35.48=1.95\\\\n=196\rightarrow UL-LL=34.02-34.98=0.96`

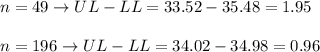
d. The width of the intervals is decreased by a factor of √4=2 when the sample size is quadrupled, while the others factors are fixed.