Question

The wheel of fortune is 2.6 meters in diameter. A contestant gives the wheel an initial velocity of 2 m/s. After rotating 540 degrees, the wheel comes to a stop. Calculate the angular acceleration of the wheel. Show your work.

Answer 1

The angular acceleration of the wheel of fortune is -0.125 radians per square second.

Step-by-step explanation:

Let suppose that wheel of fortune is decelerated at constant rate, given that wheel of fortune stops after rotating 540 degrees with an initial tangential velocity of 2 meters per second, the initial angular velocity and the kinematic expression of final angular speed as a function of angular acceleration and position are, respectively:

`\omega_(o)=(v_(o))/(R)`

`\omega^(2) = \omega_(o)^(2) + 2\cdot \alpha \cdot (\theta-\theta_(o))`

Where:

`v_(o)` - Initial tangential velocity, measured in meters per second.

`R` - Radius of the wheel of fortune, measured in meters.

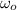`\omega_(o)` - Initial angular velocity, measured in radians per second.

`\omega` - Final angular velocity, measured in radians per second.

`\alpha` - Angular acceleration, measured in radians per square second.

`\theta` - Final angular position, measured in radians.

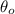`\theta_(o)` - Initial angular position, measured in radians.

Angular acceleration is now cleared in the second expression:

`\alpha = (\omega^(2)-\omega_(o)^(2))/(2 \cdot (\theta-\theta_(o)))`

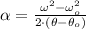
Given that
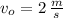`v_(o) = 2\,(m)/(s)` and
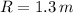`R = 1.3\,m`, the initial angular velocity is:

`\omega_(o) = (2\,(m)/(s) )/(1.3\,m)`

`\omega_(o) = 1.538\,(rad)/(s)`

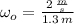
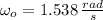
Now, if
`\omega = 0\,(rad)/(s)`,
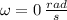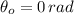`\theta_(o) = 0\,rad` and
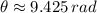`\theta \approx 9.425\,rad` (180° = π rad), the angular acceleration of the wheel is:

`\alpha = (\left(0\,(rad)/(s) \right)^(2)-\left(1.538\,(rad)/(s) \right)^(2))/(2\cdot (9.425\,rad-0\,rad))`

`\alpha = -0.125\,(rad)/(s^(2))`

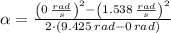
The angular acceleration of the wheel of fortune is -0.125 radians per square second.