Question

In a random sample of 300 attendees of a minor league baseball game, 182 said that they bought food from the concession stand. Create a 90% confidence interval for the proportion of fans who bought food from the concession stand. Use a TI-83, TI-83 plus, or TI-84 calculator, rounding your answers to three decimal places.

Answer 1

90% confidence interval for the proportion of fans who bought food from the concession stand

(0.5603,0.6529)

Explanation:

Step(i):-

Given sample size 'n' =300

Given data random sample of 300 attendees of a minor league baseball game, 182 said that they bought food from the concession stand.

Given sample proportion

`p^(-) = (x)/(n) = (182)/(300) =0.606`

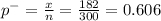
level of significance = 90% or 0.10

Z₀.₁₀ = 1.645

90% confidence interval for the proportion is determined by

`(p^(-) - Z_(0.10)\sqrt{(p(1-p))/(n) } , p^(-) +Z_(0.10)\sqrt{(p(1-p))/(n) })`

`(0.6066 - 1.645\sqrt{(0.6066(1-0.6066))/(300) } ,0.6066+1.645\sqrt{(0.6066(1-0.6066))/(300) })`

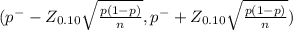
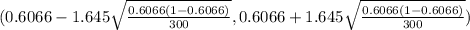
(0.6066 - 0.0463 ,0.6066 + 0.0463)

(0.5603,0.6529)

final answer:-

90% confidence interval for the proportion of fans who bought food from the concession stand

(0.5603,0.6529)