Question

Customers arrive at a movie theater at the advertised movie time only to find that they have to sit through several previews and prepreview ads before the movie starts. Many complain that the time devoted to previews is too long. A pre-liminary sample conducted by The Wall Street Journal showed that the standard deviation of the amount of time devoted to previews was 6 minutes. A. If we want to estimate the population mean time for previews at movie theaters with a margin of error of 72 seconds, what sample size should be used? B. If we want to estimate the population mean time for previews at movie theaters with a margin of error of 1 minute, what sample size should be used?

Answer 1

Using a 90% confidence level

A. A sample size of 68 should be used.

B. A sample size of 98 should be used.

Explanation:

I think there was a small typing mistake and the confidence level was left out. I will use a 90% confidence level.

We have that to find our
`\alpha` level, that is the subtraction of 1 by the confidence interval divided by 2. So:

`\alpha = (1-0.9)/(2) = 0.05`

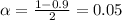
Now, we have to find z in the Ztable as such z has a pvalue of
`1-\alpha`.

So it is z with a pvalue of
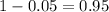`1-0.05 = 0.95`, so
`z = 1.645`

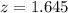
Now, find the margin of error M as such

`M = z*(\sigma)/(√(n))`

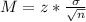
In which
`\sigma` is the standard deviation of the population and n is the size of the sample.

A. If we want to estimate the population mean time for previews at movie theaters with a margin of error of 72 seconds, what sample size should be used?

We have the standard deviation in minutes, so the margin of error should be in minutes.

72 seconds is 72/60 = 1.2 minutes.

So we need a sample size of n, and n is found when M = 1.2. We have that
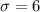`\sigma = 6`. So

`M = z*(\sigma)/(√(n))`

`1.2 = 1.645*(6)/(√(n))`

`1.2√(n) = 6*1.645`

`√(n) = (6*1.645)/(1.2)`

`(√(n))^(2) = ((6*1.645)/(1.2))^(2)`

`n = 67.65`

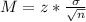
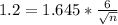
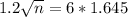
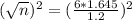
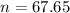
Rounding up.

A sample size of 68 should be used.

B. If we want to estimate the population mean time for previews at movie theaters with a margin of error of 1 minute, what sample size should be used?

Same logic as above, just use M = 1.

`M = z*(\sigma)/(√(n))`

`1 = 1.645*(6)/(√(n))`

`√(n) = 6*1.645`

`(√(n))^(2) = (6*1.645)^2`

`n = 97.42`

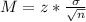
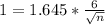
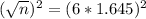
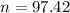
Rounding up

A sample size of 98 should be used.