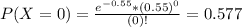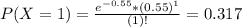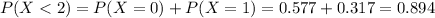Question

A local animal rescue organization receives an average of 0.55 rescue calls per hour. Use the Poisson distribution to find the probability that during a randomly selected hour, the organization will receive fewer than two calls.A) 0.087

B) 0.894
C) 0.317
D) 0.106

Answer 1

B) 0.894

Explanation:

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

In which

x is the number of sucesses

e = 2.71828 is the Euler number

`\mu` is the mean in the given interval.

A local animal rescue organization receives an average of 0.55 rescue calls per hour.

This means that
`\mu = 0.55`

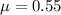
Probability that during a randomly selected hour, the organization will receive fewer than two calls.

`P(X < 2) = P(X = 0) + P(X = 1)`

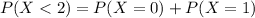
In which

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

`P(X = 0) = (e^(-0.55)*(0.55)^(0))/((0)!) = 0.577`

`P(X = 1) = (e^(-0.55)*(0.55)^(1))/((1)!) = 0.317`

`P(X < 2) = P(X = 0) + P(X = 1) = 0.577 + 0.317 = 0.894`