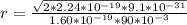Question

Medical cyclotrons need efficient sources of protons to inject into their center. In one kind of ion source, hydrogen atoms (i.e., protons with one orbiting electron) are fed into a chamber where there is a strong magnetic field. Electrons in this chamber are trapped in tight orbits, which greatly increases the chance that they will collide with a hydrogen atom and ionize it. One such source uses a magnetic field of 90 mTmT, and the electrons' kinetic energy is 1.4 eV.

Required:
If the electrons travel in a plane perpendicular to the field, what is the radius of their orbits?

Answer 1

The radius is
`r = 4.434 *10^(-5) \ m`

Step-by-step explanation:

From the question we are told that

The magnetic field is
`B = 90 mT = 90*10^(-3) \ T`

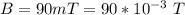
The electron kinetic energy is
`KE = 1.4 eV = 1.4 * (1.60*10^(-19)) =2.24*10^(-19) \ J`

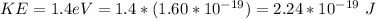
Generally for the collision to occur the centripetal force of the electron in it orbit is equal to the magnetic force applied

This is mathematically represented as

`(mv^2)/(r) = qvB`

=>
`r = (m* v)/(q * B)`

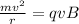
Where m is the mass of electron with values
`m = 9.1 *10^(-31) \ kg`

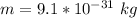
v is the escape velocity which is mathematically represented as

`v = \sqrt{(2 * KE)/(m) }`

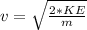
So

`r = (m)/(qB) * \sqrt{(2 * KE)/(m) }`

apply indices

`r = (√(2 * KE * m) )/(qB)`

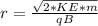
substituting values

`r = \frac{\sqrt{2 * 2.24*10^(-19)* 9.1 *10^(-31)} }{ 1.60 *10^(-19)* 90*10^(-3)}`

`r = 4.434 *10^(-5) \ m`