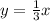Question

The given line segment has a midpoint at (3, 1).

On a coordinate plane, a line goes through (2, 4), (3, 1), and (4, negative 2).

What is the equation, in slope-intercept form, of the perpendicular bisector of the given line segment?

y = One-thirdx
y = One-thirdx – 2
y = 3x
y = 3x − 8

Answer 1

I believe the answer is A. y = 1/3x

Explanation:

Answer 2

`y=(1)/(3)x`

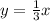
Explanation:

The given line segment has a midpoint at (3, 1) and goes through (2, 4), (3, 1), and (4, -2). We can use any two of the three points to calculate the equation of the line. Let us use the points (2, 4) and (4, -2)

Therefore the line goes through (2, 4) and (4, -2). The equation of a line passing through
`(x_1,y_1)\ and\ (x_2,y_2)` is:

`(y-y_1)/(x-x_1)=(y_2-y_1)/(x_2-x_1)`.

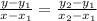Therefore the line passing through (2, 4) and (4, -2) has an equation:

`(y-y_1)/(x-x_1)=(y_2-y_1)/(x_2-x_1)\\(y-4)/(x-2)=(-2-4)/(4-2)\\(y-4)/(x-2)=(-6)/(2)\\y-4=x-2(-3)\\y-4=-3x+6\\y=-3x+10`

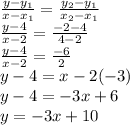
Comparing with the general equation of line: y = mx + c, the slope (m) = -3 and the intercept on the y axis (c) = 10

Two lines are said to be perpendicular if the product of their slope is -1. If the slope of line one is m1 and the slope of line 2 = m2, then the two lines are perpendicular if:

`m_1m_2=-1`.

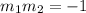Therefore The slope (m2) of the perpendicular bisector of y = -3x + 10 is:

`m_1m_2=-1\\-3m_2=-1\\m_2=(1)/(3)`

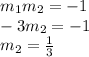
Since it is the perpendicular bisector of the given line segment, it passes through the midpoint (3, 1). The equation of the perpendicular bisector is:

`(y-y_1)/(x-x_1)=m\\(y-1)/(x-3)=(1)/(3)\\ y-1= (1)/(3)(x-3)\\ y-1=(1)/(3)x-1\\y=(1)/(3)x`

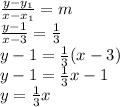
the equation, in slope-intercept form, of the perpendicular bisector of the given line segment is
`y=(1)/(3)x`