Question

Last year, a soft drink manufacturer had 22% of the market. In order to increase their portion of the market, the manufacturer has introduced a new flavor in their soft drinks. A sample of 400 individuals participated in the taste test and 100 indicated that they like the taste. We are interested in determining if more than 22% of the population will like the new soft drink. 1. Using α = .05, test to determine if more than 22% of the population will like the new soft drink. 2. What should be the critical value(s)? 3. If there is more than one, please enter the positive one. (please keep at least 4 digits after the decimal point).

Answer 1

Critical value zc = 1.6449.

As the test statistic z=1.3881 is smaller than the critical value zc=1.6449, it falls in the acceptance region and the null hypothesis is failed to be rejected.

Explanation:

This is a hypothesis test for a proportion.

The claim is that more than 22% of the population will like the new soft drink.

Then, the null and alternative hypothesis are:

`H_0: \pi=0.22\\\\H_a:\pi>0.22\\`

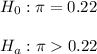
The significance level is 0.05.

The sample has a size n=400.

The sample proportion is p=0.25.

`p=X/n=100/400=0.25`

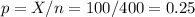
The standard error of the proportion is:

`\sigma_p=\sqrt{(\pi(1-\pi))/(n)}=\sqrt{(0.22*0.78)/(400)}\\\\\\ \sigma_p=√(0.000429)=0.0207`

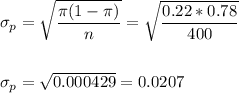
Then, we can calculate the z-statistic as:

`z=(p-\pi-0.5/n)/(\sigma_p)=(0.25-0.22-0.5/400)/(0.0207)=(0.0288)/(0.0207)=1.3881`

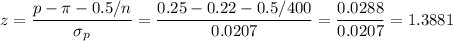
As this is a right-tailed test, there is only one critical value and it is, for a significance level of 0.05, zc=1.6449.

As the test statistic z=1.3881 is smaller than the critical value zc=1.6449, it falls in the acceptance region and the null hypothesis is failed to be rejected.